[문제]
https://www.acmicpc.net/problem/1504

조건이 있는 다익스트라 문제입니다.
해당 조건은 구현할 때 신경 써야 하는 부분은 아니므로 어려운 것은 없습니다.
단순히 주어진 정점을 반드시 찍어야 하므로, 각각에 대해서 최단 경로를 구하고 합해주면 해결할 수 있는 문제입니다.
[초기화]
def __init__(self):
self.n, self.e = map(int, input().split())
self.graph = [[] for _ in range(self.n + 1)]
for i in range(self.e):
start, end, cost = map(int, input().split())
self.graph[start].append([end, cost])
self.graph[end].append(([start, cost]))
self.v1, self.v2 = map(int, input().split())
self.inf = math.inf딕셔너리를 이용해 양방향 그래프를 만들어줍니다.
[풀이]
def dijkstra(self, start, end):
cost = [self.inf] * (self.n + 1)
pq = []
heapq.heappush(pq, (0, start))
cost[start] = 0
while pq:
current_cost, current = heapq.heappop(pq)
if cost[current] < current_cost:
continue
for nxt, next_cost in self.graph[current]:
if current_cost + next_cost < cost[nxt]:
cost[nxt] = current_cost + next_cost
heapq.heappush(pq, (current_cost + next_cost, nxt))
return cost[end]기본적인 다익스트라 구조입니다.
def solve(self):
path1 = self.dijkstra(1, self.v1) + self.dijkstra(self.v1, self.v2) + self.dijkstra(self.v2, self.n)
path2 = self.dijkstra(1, self.v2) + self.dijkstra(self.v2, self.v1) + self.dijkstra(self.v1, self.n)
print(-1) if path1 >= self.inf and path2 >= self.inf else print(min(path1, path2))두 정점을 방문해야하므로
1 → v1, v1 → v2, v2 → n에 해당하는 최단 경로를 각각 구하면 되겠습니다.
다만 1 → v2, v2 → v1, v1 → n의 경우도 함께 계산해야 합니다.
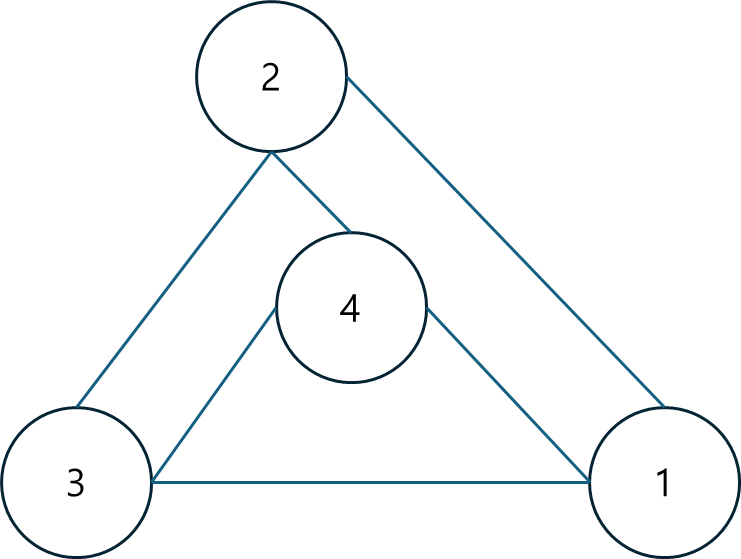
테스트케이스는 모두 연결된 상태이지만, 간선이 최대 1개가 존재한다는 조건이 있으므로 간선이 없는 경우가 있을 수 있습니다.
그렇기 때문에 두 정점에 대해 각각 이동하면서 모두 목표 정점(N)으로 갈 수 있는지 확인해야 하며, 모두 연결되어 있다면 그중 가장 최단이 되는 경로의 값을 선택해야 합니다.
[전체 코드]
import sys
import heapq
import math
input = lambda: sys.stdin.readline()
class Main:
def __init__(self):
self.n, self.e = map(int, input().split())
self.graph = [[] for _ in range(self.n + 1)]
for i in range(self.e):
start, end, cost = map(int, input().split())
self.graph[start].append([end, cost])
self.graph[end].append(([start, cost]))
self.v1, self.v2 = map(int, input().split())
self.inf = math.inf
def dijkstra(self, start, end):
cost = [self.inf] * (self.n + 1)
pq = []
heapq.heappush(pq, (0, start))
cost[start] = 0
while pq:
current_cost, current = heapq.heappop(pq)
if cost[current] < current_cost:
continue
for nxt, next_cost in self.graph[current]:
if current_cost + next_cost < cost[nxt]:
cost[nxt] = current_cost + next_cost
heapq.heappush(pq, (current_cost + next_cost, nxt))
return cost[end]
def solve(self):
path1 = self.dijkstra(1, self.v1) + self.dijkstra(self.v1, self.v2) + self.dijkstra(self.v2, self.n)
path2 = self.dijkstra(1, self.v2) + self.dijkstra(self.v2, self.v1) + self.dijkstra(self.v1, self.n)
print(-1) if path1 >= self.inf and path2 >= self.inf else print(min(path1, path2))
problem = Main()
problem.solve()'Algorithm > 백준' 카테고리의 다른 글
| [백준: Python] 18427 - 함께 블록 쌓기 (0) | 2024.11.22 |
|---|---|
| [백준: Java] 18430 - 무기 공학 (0) | 2024.11.21 |
| [백준: Python] 17141 - 연구소 2 (1) | 2024.11.19 |
| [백준: Java] 13975 - 파일 합치기 3 (0) | 2024.11.18 |
| [백준: Python] 7453 - 합이 0인 네 정수 (0) | 2024.11.17 |